LC 00456

System Dynamics (SD) was developed by Jay W. Forrester of MIT in the late fifties of the past century. This was also the time that computers were coming of age. An important asset of SD is that SD models can be simulated on a computer to get insight in a system’s dynamic behavior by means of “what-if” scenarios. SD was used to underpin the conclusions in the famous publication The Limits to Growth (Donella H. Meadows, Dennis L. Meadows, Jørgen Randers, William W. Behrens III, 1 januari 1972) by the Club of Rome in 1972. This publication showed that growth is limited due to exhaustion of natural resources. The important message was that our way of (western) life is unsustainable. Remarkably, the predictions turned out to be mostly true.

The structure of a system is determined by its elements and the relations between its elements. The inter-connectedness between elements amounts to that one element can have an effect on other elements, and so on. In this way, a system shows its behavior in the form of actions and reactions of elements. System Dynamics (SD) captures the dynamics by showing how changes in the key characteristics of elements have an effect on other elements’ characteristics. In SD jargon, the characteristics are called variables.

Research philosophy: positivism (Internal link van gemaakt. Is dat goed, of liever anders – bijvoorbeeld zoals bij de Principles (referentie naar LL 000XX)?) en Let op: verwijzing is naar een Nederlandstalige link (LC 00431) en tekst.

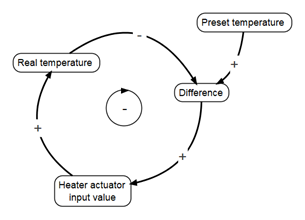
Using the thermostat as an example again, the corresponding SD model is shown below

Figure: Systems Dynamics model of a thermostat.

The variables are connected to each other with an indication of how a target variable changes as a result of a change in a source variable. The plus sign indicates that a change in a source variable induces a change in the same direction in the target variable, likewise a minus sign means a change in the opposite direction. The inclusion of a minus relation in the loop makes it a negative feedback loop, also known as a Balancing (B) loop, as is visually accentuated in the middle of the loop with the circle with an arrow containing the minus sign. Because loops play a key role, a SD model is frequently called a Causal Loop Diagram (CLD).

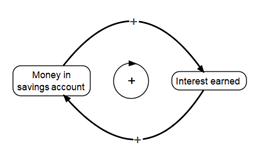
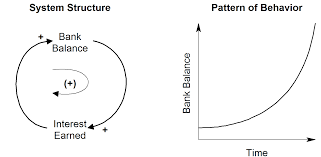
An example of a positive feedback loop, also called a Reinforcement (R) loop, is shown below. It shows how money in a savings account exponentially grows because periodically the savings are incremented with interest earned over the savings, provided the interest rate is positive. But nowadays, we are facing negative interest rates. In that case, the system still has a positive feedback loop, but unfortunately, the savings decrease exponentially.

Figure: example of a positive feedback loop.

Een alternatief dat de groei laat zien.

Figure: structure and behavior pattern of positive feedback.

SD was further popularized by Peter Senge in the Fifth Discipline (Peter M. Senge, 6 april 2006). He showed that archetypal patterns are at work as undercurrents in organizations. Frequently, wanted or unwanted results are often diagnosed for the wrong reasons because the effects of balancing and reinforcing loops behind the scene are overlooked. Recognizing the archetypal patterns at work helps to avoid making the same mistakes time and again.

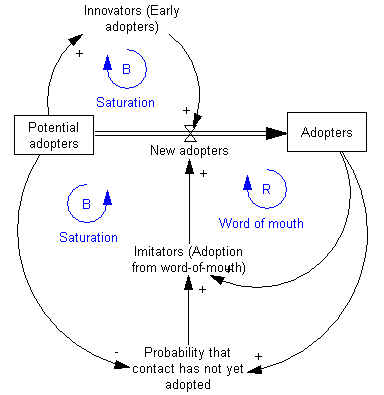
A somewhat more complex example is shown below. It is a model of how a product is adopted by customers. The model contains three interacting loops, of which two are of the balancing kind (B) and the remaining one is a reinforcing (R) loop. Two new modeling elements are included in this example: stock and flow. A stock is a reservoir in which all kind of things can be inserted and retrieved. This example features two stocks containing adopters and potential adopters. The goal is to turn a potential adopter in a real adopter. That is, to move a person from one stock to another. This transfer is modeled as a flow, and the flow rate can be influenced by all kind of factors, including … If a product is increasingly adopted and the adopters are satisfied with the product, the increase in the positive “word of mouth” feedback increases the adoption flow rate. However, as more and more potential adopters are turned over, the potential adopter stock is running dry. This has of course a negative effect on the turn-over flow rate. So, after an initial adoption rate rise, the adoption process gradually comes to an end because of lack of potential adopters.

Figure: model of how a product is adopted by customers.

Figure: model of how a product is adopted by customers.

Opmerking: Een combinatie van deze twee maken.

Geleerde les: Feedback loops

Samenvatting:
A system comprised of a number of interacting feedback loops is a complex system whose behavior can surprise us.

---

Context:
Stakeholders' worldviews may differ.

---

• Fysieke en sociale fenomenen zijn niet eenvoudig te verklaren als gevolg van de onderliggende, vaak of niet observeerbare onderstromen in de vorm van interacterende feedback loops;
• Het gevaar ligt dan op de loer dat we verkeerde conclusies trekken die leiden tot spraakverwarringen of in het ergste geval  onoverbrugbare tegenstellingen.

---

A system comprised of interacting loops is almost by definition a complex system whose behavior is difficult to understand and to predict. Reinforcing feedback loops imply exponential growths that must be somehow tamed with balancing feedback loops. The challenge is to find the sweet spot where the system stabilizes at desired levels in time and is able to absorb disruptions. The complexity can be overwhelming, and for that reason, SD models are simulated to assess their dynamic behavior.

• Lees hiervoor:
  Systems Thinking
• Lees hierna:
  Soft Systems Thinking – Soft Systems Methodology

Referenties

• The Limits to Growth, Donella H. Meadows, Dennis L. Meadows, Jørgen Randers, William W. Behrens III, Potomac Associates - Universe Books, 1 januari 1972.
• Industrial dynamics: a major breakthrough for decision makers, Forrester, J. W., Harvard business review, 36(4), 37-66., 1 januari 1958.
• Fifth Discipline: The art and practice of the learning organization, Peter M. Senge, Random House Books, 6 april 2006.

Dit is een beveiligde pagina.