Two-Valued System
We take as given the idea of distinction and the idea of indication, and that one cannot make an indication without drawing a distinction. We take, therefore, the form of distinction for the form.This is a rather mysterious, circular definition which will become more clear after the ideas behind LoF have been gradually exposed. Spencer-Brown then goes on by giving a definition of distinction.
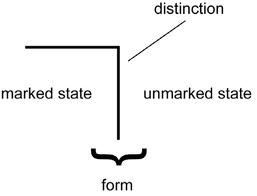
Definition: distinction is perfect continence.A distinction is made by drawing a boundary that severs a space in two sides. It is not possible to go from one side of the boundary to the other one without crossing the boundary. The first boundary that is drawn is called the first distinction. One side of the distinction is marked, and the other one is unmarked. Crossing a boundary implies that an opposite state is reached.
Elaborating on the definition “Distinction is perfect continence.”, a two-valued (marked and unmarked) mathematical system is developed based on two axioms (i.e., they are laws that are taken for granted and cannot be proofed as a logical consequence of some premises).
The law calling is defined as: the value of a call made again is the value of the call. The law of calling can be justified by stating that it does not matter if a name of someone or something is called many times. It all amounts to call just once.
The law of crossing is defined as: the value of a crossing made again is not the value of the crossing. Suppose you are blindfolded and positioned somewhere randomly in the form in a state that is either marked or unmarked. Let’s assume it is the marked state, but it could as well have been the unmarked state. Now cross a boundary, which will bring you from the marked state to the unmarked state. Now again, cross a boundary. This will bring you back to the original marked state. It does not matter if in the second turn the same boundary is crossed or a not. Crossing a boundary twice cancels the two crossings since the same state is reached. You, as a blindfolded person, cannot tell which boundaries have been crossed. Therefore, for any boundary, to re-cross is not to cross.
Instead of using a circle as a symbol of distinction, the mark of distinction is used, which captures the notion of distinction and indication in one symbol. The vertical bar of the symbol stands for the boundary. The horizontal bar represents the marked or indicational space of a severance. As we will see, the notion of an indicational space is essential for understanding self-referential forms that will be discussed later on.
The mark of distinction indicates several things at once:
- the outside (emptiness, void, nothing, the unmarked state);
- the inside (something, the marked state);
- the distinction as a sign (indication);
- the distinction as an operation of making a distinction;
- the observer, the one that makes the distinction.
The mark of distinction is both an operator (an injunction to cross) - and an operand (an indication having a value). The laws of calling and crossing can be expressed with the mark of distinction as follows.
- [math]\displaystyle{ \begin{array}{llcll} \mbox{Law of calling:} & \overline{\;\;|}\;\overline{\;\;|} & = & \overline{\;\;|} & \mbox{(marked state)} \\ \mbox{Law of crossing:} & \overline{\overline{\;\;|}\Big|} & = & & \mbox{(unmarked state, represented as a space)} \end{array} }[/math]
With these two laws, a two-valued mathematical system is elaborated that consists of an arithmetic (called the primary arithmetic) and an algebra (called the primary algebra). These two together form the calculus of indications. The calculus can be used to interpret Boolean algebra. Because of this possibility, some critics have dismissed LoF as just another form of Boolean algebra albeit one with a concise notation. This criticism misses the mark (no pun intended). LoF should be regarded as a protologic, a formalism concerned with or relating to origins or beginnings (see: space is the place (Michael Schultz, 1 januari 2009)).
An impression of how Boolean logic can be interpreted in the calculus of indications is given here in order to make the idea of self-reference, which is the subject matter of the next section, more accessible.
- [math]\displaystyle{ \begin{array}{cccl} \overline{\;\;|} & \stackrel{def}{=} & True & \mbox{corresponding with the marked state} \\ & \stackrel{def}{=} & False & \mbox{corresponding with the unmarked state} \end{array} }[/math]
The common Boolean operators not, and, or, and implies are shown In the truth-table below.
| [math]\displaystyle{ A }[/math] | [math]\displaystyle{ B }[/math] | [math]\displaystyle{ not A \stackrel{def}{=} \overline{A|} }[/math] | [math]\displaystyle{ A\;and\;B \stackrel{def}{=} \overline{\overline{A|}\;\overline{B|}\Big|} }[/math] | [math]\displaystyle{ A\;or\;B \stackrel{def}{=} AB }[/math] | [math]\displaystyle{ A \rightarrow B \stackrel{def}{=} \overline{A|}B }[/math] |
|---|---|---|---|---|---|
| [math]\displaystyle{ \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\overline{\;\;|}\;\overline{\;\;|}\Big|} = \overline{\overline{\;\;|}\Big|} = }[/math] | [math]\displaystyle{ \overline{\;\;|} }[/math] | |||
| [math]\displaystyle{ \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\overline{\;\;|}\;\overline{\overline{\;\;|}\Big|}\Bigg|} = \overline{\overline{\;\;|}\Big|} = }[/math] | [math]\displaystyle{ \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\;\;|}\;\overline{\;\;|} = \overline{\;\;|} }[/math] | |
| [math]\displaystyle{ \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\overline{\;\;|}\Big|} = }[/math] | [math]\displaystyle{ \overline{\overline{\overline{\;\;|}\Big|}\;\overline{\;\;|}\Bigg|} = \overline{\overline{\;\;|}\Big|} = }[/math] | [math]\displaystyle{ \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\overline{\;\;|}\Big|} = }[/math] | |
| [math]\displaystyle{ \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\overline{\;\;|}\Big|} = }[/math] | [math]\displaystyle{ \overline{\overline{\overline{\;\;|}\Big|}\;\overline{\overline{\;\;|}\Big|}\Bigg|} = \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\;\;|}\;\overline{\;\;|} = \overline{\;\;|} }[/math] | [math]\displaystyle{ \overline{\overline{\;\;|}\Big|}\;\overline{\;\;|} = \overline{\;\;|} }[/math] |